77. 组合

给定两个整数 n 和 k，返回范围 [1, n] 中所有可能的 k 个数的组合。你可以按 任何顺序 返回答案。

示例 1：

输入：n = 4, k = 2
输出：
[
  [2,4],
  [3,4],
  [2,3],
  [1,2],
  [1,3],
  [1,4],
]
示例 2：

输入：n = 1, k = 1
输出：[[1]]
[具体题目链接](https://leetcode-cn.com/problems/combinations/)

Python

class Solution:
    def combine(self, n: int, k: int) -> List[List[int]]:
        res = []
        tmp=[]
        #以下有tmp两种方法，代码以全局来写，注释为传参
        def backtrace(i):#传参：backtrace(ii,tmp)
            if len(tmp)<k-(n-i+1):#如果长度够不则终止，剪枝
                return
            if len(tmp) == k:#如果数目够了则储存
                res.append(tmp[:])#切片，传参：res.append(tmp)
                return
            #下面是选择
            tmp.append(i)#此处采取全局变量形式，因此需要进行添加和移除工作。
            backtrace(i+1)
            tmp.pop()
            #下面是不选择
            backtrace(i+1)
            #以上四行行采用传参的写法
            #backtrace(i+1,tmp+[i])
            #backtrace(i+1,tmp)
        backtrace(1)#传参，backtrace(1,tmp)
        return res

思路：图片来自于讲解点击直达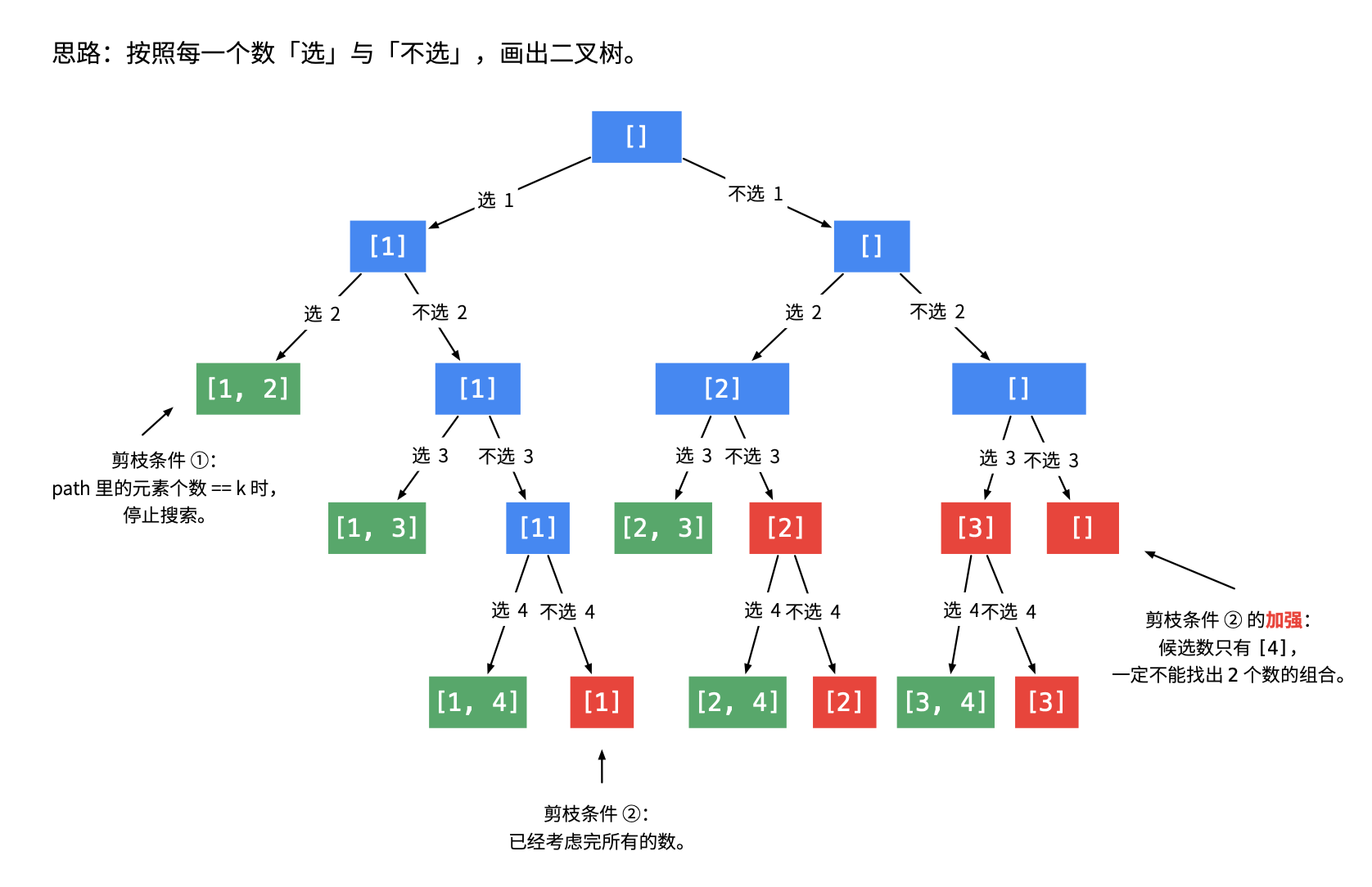

每次回溯都做出两个选择，选择当前元素和不选择当前元素，每当tmp达到预定长度则res进行记录。选择当前元素则要进行记录，并进行下一轮回溯，而不选择当前元素则直接进入下一轮回溯。(深度优先搜索)

class Solution:
    def combine(self, n: int, k: int) -> List[List[int]]:
        res = []
        def backtrace(i,tmp):
            if len(tmp) == k:
                res.append(tmp)
                return
            for j in range(i,n+1):
                if len(tmp)<k-(n-i+1):break
                backtrace(j+1,tmp+[j])
        backtrace(1,[])
        return res

思路：图片来自于讲解点击直达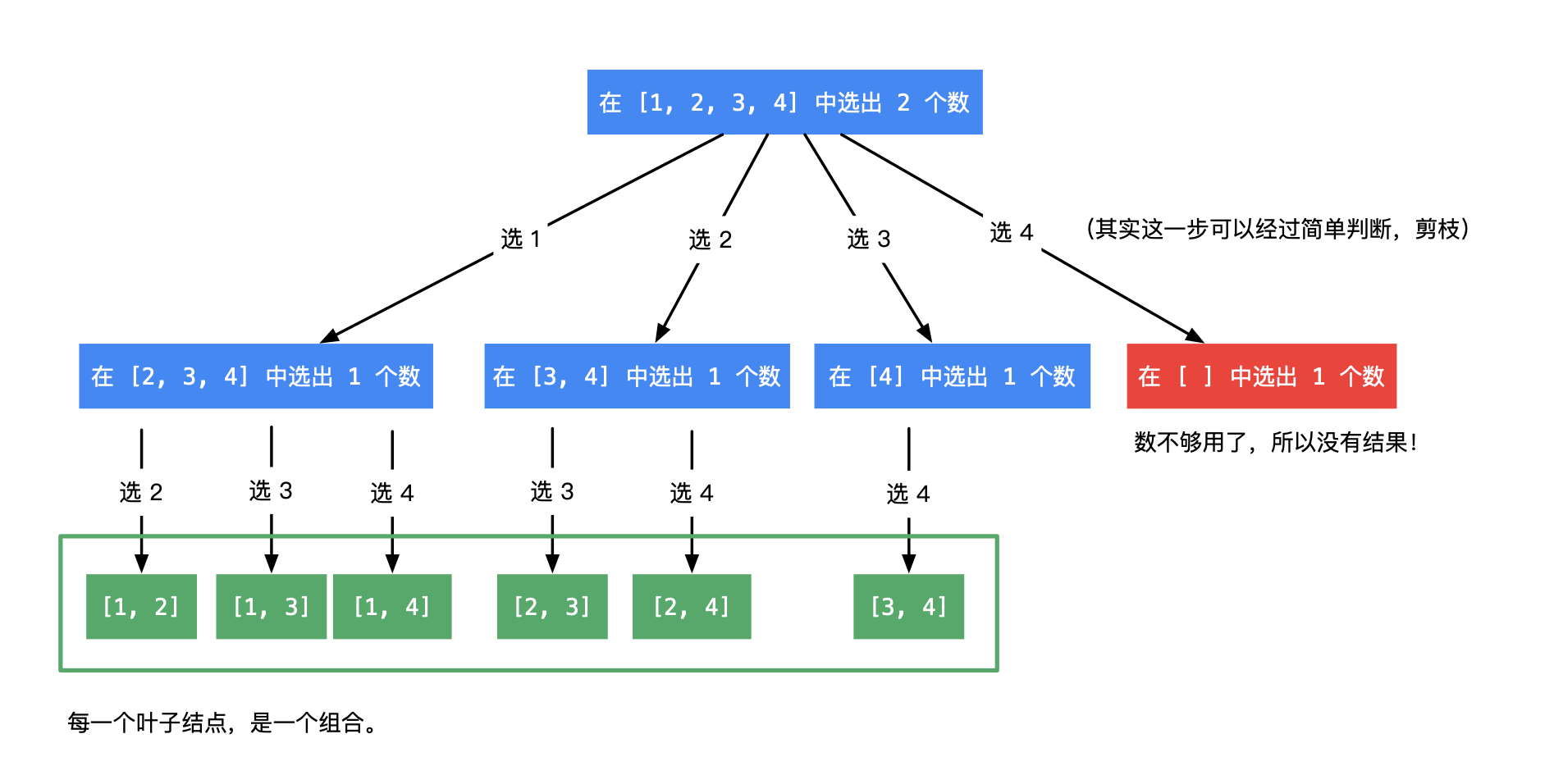

每次for循环都将剩余的元素依次选择，例如n=4，k=2[1,2,3,4]，选中1后tmp=[1]，则要在[2,3,4]中在寻找一个，所以所有1开头的组合就是[1,2],[1,3],[1,4],若选中2则是[2,3],[2,4],以此类推。

GO

func combine(n int, k int) [][]int {
    res := [][]int{}
    res = def(1, k, n, []int{}, res)
    return res
}
func def(i, k, n int, tmp []int, res [][]int) [][]int {
    if len(tmp) == k {
        res = append(res, tmp)
        return res
    }
    for j := i; j <= n-(k-len(tmp))+1; j++ {
        tmp1:=[]int{}
        tmp1 = append(tmp1,tmp...)
        tmp1=append(tmp1,j)
        res = def(j+1, k, n, tmp1, res)
    }
    return res
}

思路：思路同python第二个代码，不同之处在于go没有在函数内定义函数。需要传参，数组传参采用值传递，但是我在使用过程中，发现了有的问题因此需要注意，不知道原因。例如将以下代码

        tmp1:=[]int{}
        tmp1 = append(tmp1,tmp...)
        tmp1=append(tmp1,j)
        res = def(j+1, k, n, tmp1, res)

改为

res = def(j+1, k, n, append(tmp,j), res)

虽然有的可以出正确结果，但有的不可以。查看地址发现出问题的是因为地址相同，导致覆盖，但是其他的却没有地址相同，所以发生了引用传递的情况，原因未知。等以后解决

46. 全排列

给定一个不含重复数字的数组 nums ，返回其 所有可能的全排列 。你可以 按任意顺序 返回答案。

示例 1：
输入：nums = [1,2,3]
输出：[[1,2,3],[1,3,2],[2,1,3],[2,3,1],[3,1,2],[3,2,1]]
示例 2：
输入：nums = [0,1]
输出：[[0,1],[1,0]]
示例 3：
输入：nums = [1]
输出：[[1]]

具体题目链接

Python

class Solution:
    def permute(self, nums: List[int]) -> List[List[int]]:
        res=[]
        length=len(nums)
        def dfs(start=0):
            if start==length:
                res.append(nums[:])
                return
            for i in range(start,length):
                class Solution:
    def permute(self, nums: List[int]) -> List[List[int]]:
        res=[]
        length=len(nums)
        def dfs(start=0):
            if start==length:
                res.append(nums[:])
                return
            for i in range(start,length):
                nums[start],nums[i]=nums[i],nums[start]
                dfs(start+1)
                nums[start],nums[i]=nums[i],nums[start]
        dfs()
        return res

思路：全排列，则就不断调换nums数组内的顺序。代码通过nums[start],nums[i]=nums[i],nums[start]实现nums数组的改变和还原。

GO

func permute(nums []int) [][]int {
    length:=len(nums)
    res:=[][]int{}
    var dfc func(start int)
    dfc=func(start int){
        if start==length{
            newnums:=make([]int,length)
            copy(newnums,nums)
            res=append(res,newnums)
            return 
        }
        for i:=start;i<length;i++{
            nums[start],nums[i]=nums[i],nums[start]
            dfc(start+1)
            nums[start],nums[i]=nums[i],nums[start]
        }
    }
    dfc(0)
    return res
}

思路：同python

784. 字母大小写全排列

给定一个字符串S，通过将字符串S中的每个字母转变大小写，我们可以获得一个新的字符串。返回所有可能得到的字符串集合。

示例：
输入：S = "a1b2"
输出：["a1b2", "a1B2", "A1b2", "A1B2"]

输入：S = "3z4"
输出：["3z4", "3Z4"]

输入：S = "12345"
输出：["12345"]

具体题目链接

Python

class Solution:
    def letterCasePermutation(self, s: str) -> List[str]:
        length=len(s)
        res=[]#深度优先搜索-回溯法
        def dfs(start,tmp):
            if start==length:
                res.append(tmp)
                return 
            if s[start].isalpha():
                dfs(start+1,tmp+s[start].upper())#大写
                dfs(start+1,tmp+s[start].lower())#小写
            else:
                dfs(start+1,tmp+s[start])
        dfs(0,'')
        return res

思路：深度优先搜索-回溯法，即完成一个排列再去完成下一个排列。

class Solution:
    def letterCasePermutation(self, s: str) -> List[str]:
        res=['']
        length=len(s)
        for i in range(length):#广度优先搜索
            for j in range(len(res)):
                if s[i].isalpha(): 
                        res.append(res[j]+s[i].lower())
                        res[j]=res[j]+s[i].upper()   
                else:
                        res[j]=res[j]+s[i]
        return res

思路：广度优先搜索方法，每次循环都向res内所有字符串添加一个字符。若字符为字母，则会新创建len(s)个字符串（复制res），实现大小写的两种状态。

class Solution():
    def letterCasePermutation(self, S):
        B = sum(letter.isalpha() for letter in S)
        ans = []
        for bits in range(1 << B):
            b = 0
            word = ''
            for letter in S:
                if letter.isalpha():
                    if (bits >> b) & 1: 
                        word=word+letter.lower()
                    else:
                        word=word+letter.upper()
                    b += 1
                else:
                    word=word+letter
            ans.append(word)
        return ans

思路：官网的二进制枚举方法，仔细看了下。先统计字符串的字母的个数。之后通过(1 << B)计算出共有多少种状态，相当于2^B.
(bits >> b) & 1整体意思：word中要改变字母大小写的个数。
分开看(bits >> b)意思是能改变几个字母的状态：例如当bits为0或1时，对应二进制'0','1'，属于同一位，位数代表可改变的字母个数。或bits为2，3时，对应二进制就是'10','11'，位数为2，则改变两个字母。
(bits >> b) & 1其中的& 1则表示，每一位中（对应一个字母）要有一位转为大写(0&1)=0，一位转为小写(1&1)=1。

GO

func letterCasePermutation(s string) []string {
    length:=len(s)
    res:=[]string{}
    var dfs func(tmp string,start int)
    dfs=func(tmp string,start int){
        if start==length{
            res=append(res,string(tmp))
            return
        }
        if (s[start] >= 'a' && s[start] <= 'z') || (s[start] >= 'A' && s[start] <= 'Z'){
            dfs(tmp+string(s[start]^(1 << 5)),start+1)
        }
        dfs(tmp+string(s[start]),start+1)
        
    }
    dfs("",0)
    return res
}

思路：同python代码，代码a^(1 << 5)（a）是字符，意思是若大写则小写，若小写则大写。